Where am I?

A simple look at navigating by the stars.

With the advent of Satnav and GPS and the ever increasing affordability of the devices needed, the art of astronavigation is slowly dying.

However there is an atavistic pleasure in being able to work out one's position using the traditional sextant and chronometer.

This is not going to be a detailed treatise on how to do that, but rather an explanation of first principles, a whetting of the appetite to the methodologies employed to determine a position on the earth independent of external navigational aids.

Fix versus position

Strictly speaking a "fix" is defined as a position obtained from fixed terrestrial objects while a "position" is that obtained from the moving celestial objects. However many people talk of a celestial "fix".

What do I need?

A device to measure angles - in most cases a sextant, an accurate chronometer, a set of current astronomical tables, a compass, a pencil, ruler, protractor and some scrap paper. And knowledge of how to use them.

We will look at the mechanics of these devices later.

Spheres within spheres

Firstly let us have a look at the theory of the subject. I want you to visualize the earth as a sphere rotating within another sphere on which all the celestial bodies (stars, planets, sun and moon) have been painted. At any given moment there is somewhere on earth where a given celestial body is right overhead - 90°. What is technically called the "zenithal point".

Now if we know the exact position where this "dead overhead" occurs and the exact time it happens we can calculate our distance to that point by measuring the angular distance we are from that celestial body at that time. If we do this for three such bodies simultaneously then we can draw three circles on a map and where they intersect is where we are!

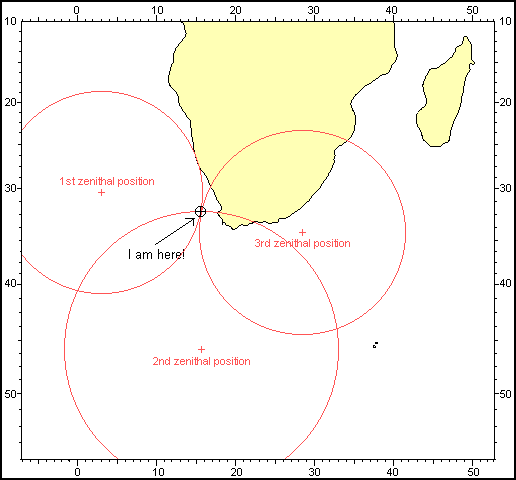And astonishingly that's all there is to it!

Now for the BAD news

The mechanics involved are a little more complicated.

Let us first look at how a position on the face of the earth is determined.

Latitude

Imagine the earth as a large apple. Slice the apple at regular intervals at right angles to the core. These slices would be something like the lines of latitude. Latitude is a "natural" measure insofar as it is determined by an angular measurement from the centre of the earth. The line that cuts the earth in half is known as the equator (0°) and the poles are at 90°. The angular measurement from the centre of earth determines the lines of latitude on its surface.

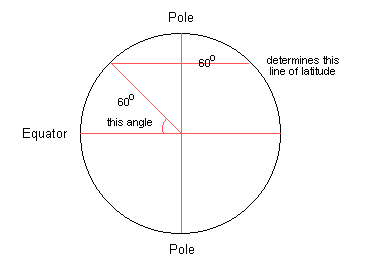An added advantage is that one minute of latitude is equivalent, for all practical purposes, to 1 nautical mile. 1 degree to 60 nautical miles. A nautical mile is 1854 metres, for the metrically inclined.

It has always been fairly easy to find one's latitude from the position of the sun or, if in the Northern hemisphere, from the pole star.

Longitude

Imagine the earth as a large orange. Slice the peel into gores as if you were about to peel it. These "slices" equate to the lines of longitude. Longitude is a "man made" measure insofar that the line from which all longitude is measured is the line that runs through the old naval observatory in Greenwich. Longitudinal distances are related to time and every 15° is the distance the earth rotates in one hour. The distance of a degree of longitude varies with the place on earth it is measured.

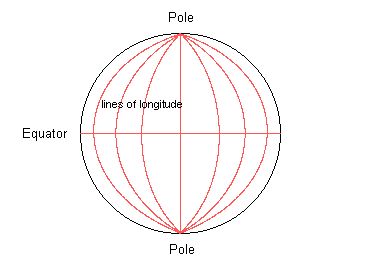By determining one's latitude and longitude a position anywhere on earth can be described.

The tools

The sextant allows determination of zenithal distance to the sub-stellar point of a celestial body, the chronometer allows determination of the exact time of the above and the almanac allows determination of where that sub-stellar point was at the observed time. The compass allows a bearing to the point to be determined and the chart is where all these come together to allow us to determine our position.

In theory.

In practice the distances are too great to mark off on a chart with any accuracy, and charts, being flat representations of a spheroid (oblate spheroid for the purists) introduce complexities and errors all of their own.

So how is it done?

In practice a number of methods are employed. Most of these rely on one having a fair approximation of one's latitude and longitude. An assumed or deduced position. I will briefly describe one of the more popular methods:

Enter Marcq St Hilaire

In the Marcq St Hilaire method, using spherical trigonometry and an assumed or deduced initial position what one does is work out what the zenithal distance should be if the assumed position was accurate. One then subtracts or adds the differences from the true zenithal distances to obtain the true position.

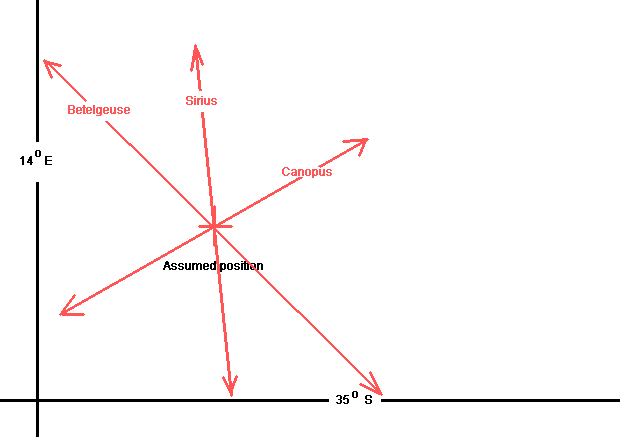We have "shot" three stars - Betelgeuse, Sirius and Canopus. We have corrected for time lapse (and movement if on a moving object) and have drawn, on a piece of paper - to scale - our assumed position. If we were exactly there, the three circles would intersect there. The lines in red are the parts of the circles that should be intersecting. They are seen here as straight lines because at the distances involved the slight curvature is of minor importance. However we have done our calculations and found, as we expected, the zenithal distances are not exactly passing through our assumed position.

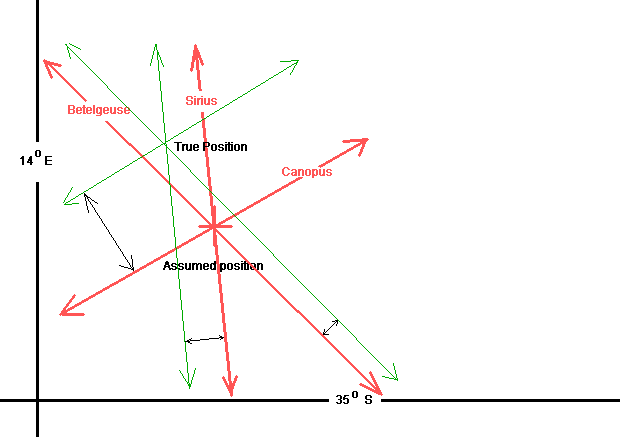By adjusting our lines towards or away from (as the calculations show) the assumed lines we find a new intersection - which is our true position. In practice the assumed position is desired to be as close to the true as possible. If it is badly in error a new assumed position can be used and the star sights recalculated. One usually uses the new position shown by the calculations for this. By doing this successively a pretty accurate position can be obtained.

Some limitations

An accurate position can only be found at morning and evening twilight when both the celestial bodies and the horizon are visible when using an ordinary nautical sextant. If the weather permits observation of these! A position line can be determined from the sun, successive such lines can give a fair position - and if the moon is visible during daylight by some manipulations a fairly accurate position can be determined. A position can be obtained by the so-called "noon sight". Sometimes, with a bright moon, the horizon can be seen at night permitting star sights.

Under ideal conditions and expert handling of the sextant a postion can be found that is less than a mile in error.

Conclusion

I hope this short little page will have sufficiently whetted your appetite to want to know more. There are many volumes available explaining the science of astronavigation - a good yachting supplier should have any number of these. A smattering of mathematics is needed - but an astro calculator can replace even that knowledge. I have a cousin who sailed the oceans as a yachtsman for years who had not the slightest idea of the math involved - relying on a calculator to translate his sextant readings into something he could plot on a chart!

And to give some idea to the really curious I include a worked example to show how it's done.

A note on astronavigation on land as opposed to at sea.

Take an imaginary cruise and experience the star sights.

And finally, all the spherical trigonometry you need to know!