The chart

No chart or map of the face of the earth is accurate. The very attempt to portray a portion of a sphere on a flat surface is fraught with difficulties. Charts attempt to be correct in some detail or at some points but are in error at others. The chart most used for navigation is the Mercator chart. Mercator's projection has some horrendous distortions as to shape, area and scale but it has one property mariners prize above all others - a line of bearing on the chart is equal to the compass course between two points. It is not the shortest distance, but it will get you there!

Most charts are "projections" in that they are supposed to represent on a flat plane a projection of a point on the surface of the earth. Charts attempt to emphasise one of the following qualities:

• preservation of area
• preservation of shape
• preservation of scale
• preservation of bearing

To achieve any one of these qualities the rest must be, to some degree, sacrificed.

In the Mercator projection, preservation of bearing is all important and scale, shape and area are progressively distorted as the latitude increases.

Mercator projections are "cylindrical" projections insofar as they are derived by imagining a large sheet of paper wrapped about the earth in the form of a cylinder. For this example we will imagine this sheet touching the earth only at the equator. Then, from the center of the earth, we will draw lines through features on the surface of the globe and continue those lines until they strike the paper cylinder.

Notice how features A, B, C and D are projected onto the paper at A', B', C' and D'. Observe the distortion as to distance between A and B and A' and B'.

It is easy to see that the poles can never be represented on such a chart and that the distortions inherent at higher latitudes make the area and shapes of such features as Greenland wholly untenable. Scales, too, become impossible and at higher latitudes great care must be exercised and correct scales calculated for every latitude.

Mercator's projection is not a simple cylindrical projection as depicted above but a mathematically developed one so as to preserve a specific ratio between the latitude and longitude.

As mentioned previously the Mercator chart allows a loxodrome - or line of constant bearing - to be drawn on it as a straight line between two points. Such a line cuts every line of longitude at the same angle.

Great Circles are arcs on a Mercator chart. Except the for the equator and for lines of longitude.

One other chart is occasionaly used by mariners and that is the Gnomonic projection - this chart allows Great Circles to be drawn as straight lines. It is however even more complicated than a Mercator projection and bearings must be calculated for every position of the chart as no compass rose can be shown on such a chart - except for one particular point.

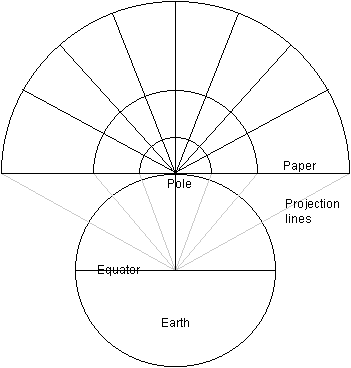Gonomonic projections, or variants thereof, are frequently used to depict the polar areas in Atlases as these areas lend themselves well to such projections.