Spherical TrigonometryWe saw how 1 minute of arc on the face of the earth was equal to 1 nautical mile. We also saw how the position of any two places on the globe can be described by means of their latitude and longitude.
The triangle!Assuming we have two places - call them A and B because its traditional - and we wish to determine how far they are from each other.
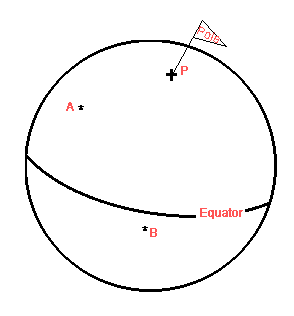 The first thing we do is work out their Polar Distance - that is we find out their angular distance to the North pole. If the latitude is in the northern hemisphere we subtract it from 90 and if it is in the southern hemisphere we add 90 to it. This gives us the angular measures PA and PB - which are two sides of the triangle APB.
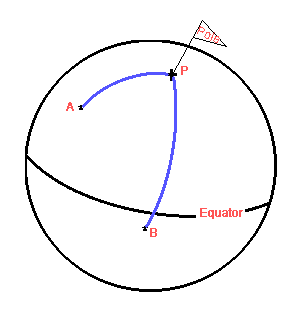 Next we work out their Polar Angle. If both longitudes are in the same hemisphere we subtract the smaller from the larger - if they are in different hemispheres we add them. With the proviso that if the answer is greater than 180° we will subtract it from 360.
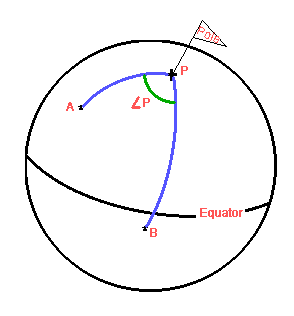 We now have two sides and an angle - and having that we can solve for the rest of the triangle using spherical trigonometry.
The first two formulae:I use haversines - which is a contraction of half-versed sines - for ease as they handle angular measures up to 180° without any problems. So if we have an angle A and wish to convert it to a haversine we use the following little formula which any trig calculator should be able to do in a jiffy:
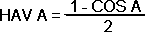 And if we have a haversine A and wish to convert it to an angle the following formula will do it:
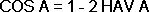
The next two formulae:These formulae will allow you to solve for the distance AB and for the angle A (or B with some manipulation).
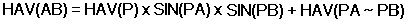 The tilde ~ is used to denote "the difference between". In other words always subtract the smaller from the larger.
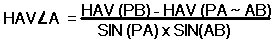
Down to practical thingsWe have the following two places on earth. How far are they apart?
 The polar angle is 15° East + 30° West - different hemispheres so we add. Thus the polar angle is 45°. A is in the North so we subtract from 90 which is 90 - 15 = 75° while B is in the South so we add 90 to it which gives 90 + 15 = 105°. To sum up we have the following:
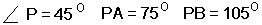
Let's turn some of these numbers into haversines and sines:
If we plug these numbers into the first haversine formula we get:
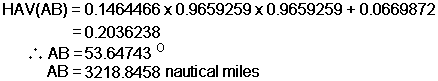 Remember to convert degrees to nautical miles you multiply by 60. And to solve for the angle A we use the second formula:
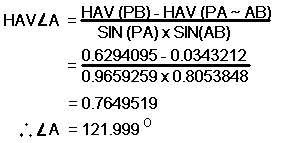 By simply reversing A and B we can solve for B as well!
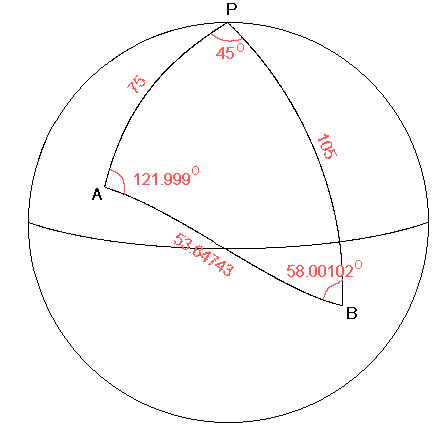 And there the whole spherical triangle is solved. Master that and there is little in navigation that will defeat you, mathematically!
|