Powering of Hulls - a simple discussionEasy questions - very difficult to answer exactly. There is no such thing as a "top speed" for any given hull/powerplant combination. Many factors affect the speed of any hull and only by stating them can an absolute "top speed" for those conditions be given. Some factors affecting the speed are:
Any statement about the speed of a hull which does not define most of the above conditions is pretty valueless. A ship in fresh water at 30 degrees C with an air temperature of 35 degrees C at light load will perform differently to one in seawater at 8 degrees C with an ambient temperature of 11 degrees C while fully laden. There are basically four forces that have to be overcome to move a hull through water. These are:
In practice Air Resistance is quite minimal - accounting for a few percent of the total resistance, usually less than 5%. However the faster a hull is moved the greater this resistance becomes. Eddy-making resistance is quite small and in a well designed hull is negligible. It is quite often combined with Wave-making resistance. Wave-making resistance is extremely important and it increases dramatically with speed. This is the power the ship expends making all those nice foamy wakes etc. Frictional resistance is that part of the resistance created by the effect of the hull "rubbing" against the fluid it is moving through. Some formulasFroude stated that frictional resistance is dependent on the following four factors:
Froude derived a formula :
To derive the wetted area I have elected to use Taylor's formula
Where:
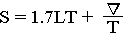
Where:
ExampleWe have the following parameters - calculate frictional resistance:
Wetted area will be (Taylor) 2.58 x square root of 90000 x 312 which equals 13671.6 square metres. Call it 13671 to make calculations easier. Frictional resistance will be (Froude) 1.386 x 13671 x 15.432 to the power 1.825 or 2795336.7 newtons. Call it 2795 kiloNewtons (kN) for simplicity. To obtain the effective horsepower to overcome this component of the resisting forces we simply multiply it by the speed in metres per second to get kiloWatts (kW). Thus 2795 x 15.432 = 43132 kW or 57842 horsepower. 1 horsepower is equal to 0.7457 kW. Effective horsepower is not shaft horsepower but that power delivered by the screws. There is a loss in efficiency between SHP and Effective horsepower which varies according to propellor design and speed. Having derived the formula for this hull it becomes very easy to draw up a table for the hull at various speeds.
As we can see the frictional component rises sharply as speeds increase - which was to be expected. Of the four components of total resistance we now have derived one - frictional resistance. Frictional resistance plays a large role in the total resistance but this gets less and less as the speed increases. At higher speeds wave-making resistance becomes the major component in the total resistance a hull offers to forward motion.
Wave-making resistance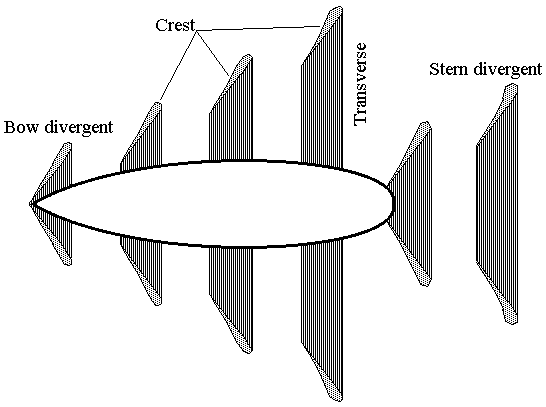
When a body moves through a fluid it displaces that fluid and the displacement takes energy to effect. The calculation of the amount of resistance that wave-making causes is fraught with difficulty. It is determined by towing tank observations or complex modelling programs run on fast computers. An excellent paper on this is available here. We are trying to keep it simple - so in fact what we are looking for is a simple rule-of-thumb type formula that will give us a ballpark figure. See Greg Locock's page for further discussion on this subject. We know, from experience with existing ships, that the residual resistance at 35 knots averages about 60% of the total offered and at 40 knots it is approaching 70%. Thus in our previous examples of 35 knots taking 89379 effective horsepower to overcome frictional resistance and 40 knots requiring 130335 we could expect a total of around 223447 and 434450 effective horsepower respectively. If we take a propellor efficiency of around 80% then we are looking at perhaps 279308 shp and 543062 shp respectively to move our example hull at these speeds. This ties in fairly well with known hull/power/speed combinations. The graph:
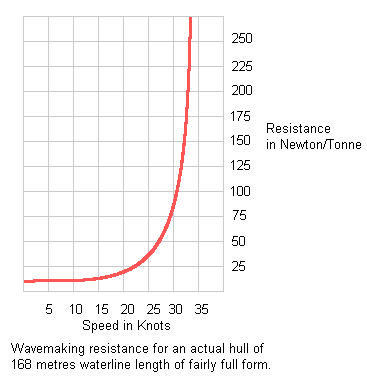
Is for an actual cargo vessel. It shows the wave-making resistance at various speeds expressed as a force per tonne. Thus at about 20 knots, this particular vessel's top cruising speed, one could expect the wave making resistance to equal 25 Newton per tonne, or, as she was a 12500 tonne vessel, a total of 312.5 kN. Notice how rapidly the curve rises so that by 30 knots the drag now equates to 937.5 kN. The power to overcome these two forces would be 4300 horsepower and 19400 horsepower respectively. Using the earlier formulae to calculate frictional resistance we find that at 20 knots this would be 372 kN and at 30 knots 780 kN. And the effective power needed to overcome that would be in the region of 5100 hp and 16100 hp respectively. Or totals of 9400 hp and 35500 hp. Adding air and eddy-making resistance as an arbitrary 5% we would now have 9870 and 37275 effective horsepower. Given an arbitrary propellor efficiency of 80% then the shaft horsepower needed will be 12340 and 46600 respectively. Thus to achieve a speed advantage of 10 knots an extra 35 000 shp is needed. This particular vessel, a fast reefer, was fitted with a 16000 horsepower MAN diesel engine and achieved a speed slightly greater than 22 knots on her measured mile trials with a clean hull, standard displacement, ambient sea temperature of 12 degrees and an ambient air temperature of 19 degrees. And our calculations have shown that calculated and actual powering were near enough each other to be confident that we could predict this within a few thousand horsepower - knowing little more of the hull than its tonnage and length.
Comparison.One of Froude's earliest observations was that when two similarly shaped bodies of differing lengths are moved through water they both produce the same pattern of waves but at differing speeds. Thus, for example, a 5.5 metre hull will produce the same pattern of waves at 9 knots that a 22 metre hull will produce at 18 knots. This was an enormously important discovery as it produced a formula that allowed tank-testing of models to ascertain their wave making resistance and then have that scaled up to a full sized ship. For the very first time the design of hulls was put on a scientific footing and engineers could, with a great degree of confidence, guarantee the speed/power combinations of given hulls. Today complicated computer-driven modelling programs can eliminate much of the physical tank testing which saves much time and money during initial design work. All of this brings us to that old rule-of-thumb formula: Hull speed in knots = 1.3 x sqrroot(waterline length in feet). I want to discuss this at some length. The actual formula, as popularised by a book on Yacht design published in the early sixties, is: Hull speed in knots = C x sqrroot(waterline length in feet) where C is a constant varying with form. Yachtsman usually take it as 1.34 but it varies from about 1.42 for fine hulls to 1.18 for chunkier ones. It only pertains to displacement hulls and gives an approximation of the maximum speed a hull can achieve before the bow wave combines with the stern wave to dig a trough out of which the vessel would not be able to climb without using inordinate amounts of power. The formula needs to be used circumspectly and applied to hulls within reasonable limits. It cannot be used indiscriminately to prove absolute values for any hulls. The absurdity becomes apparent when a hull of infinte length is inserted into the formula. It is not self limiting. Thus a hull of a few millimetres could almost not move while an infinte one could move infintely fast. In fact the formula is not much use above about 200 feet and is in fact best utilised on small sailing dinghies. In fact the ocean literally teems with vessels exceeding their "hull speed" according to this formula. See here for more details. A formula that used to be used (and may still be for all I know) in preliminary design work to determine the length of a ship to avoid the problem of "hull speed" was:
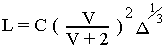
Where:
However this is not a very scientific way of going about finding some easy method to calculate an approximate maximum speed of a given hull/powerplant combination. The greatest stumbling block is the determination of wave-making resistance by a reliable yet easy method - so if anyone out there has some rule-of-thumb type method of approximating the wave-making resistance of a hull, I invite them to add their voice to this by e-mailing me at [email protected].
|
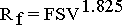that allows a close approximation of the frictional
resistance to be made.
Where
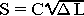because we are primarily interested in fast
hulls.
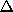= displacement in tonnes
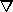= volume of displacment in cubic metres
